The Problem
The problem in question is located here. Basically, its premise is that you are given a hexagonal grid like this:
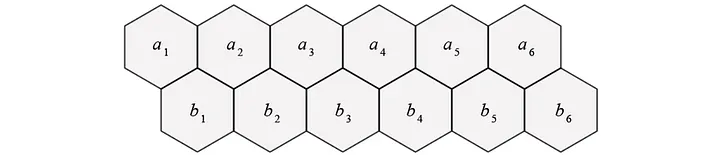
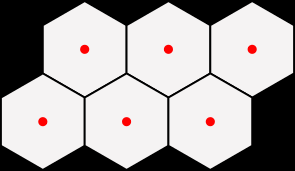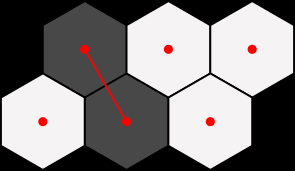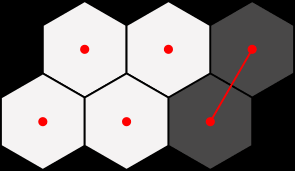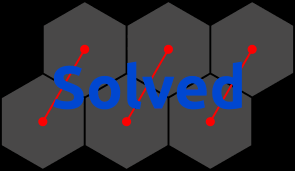
You are then required to create tiles out of the grid by pairing any two adjacent hexagonal cells as illustrated below:
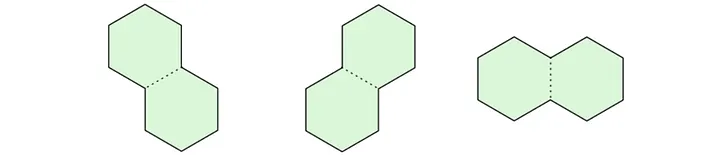
Your goal is to see whether you can successfully manage to tile all the cells in the given grid. To complicate matters, some cells are blackened:
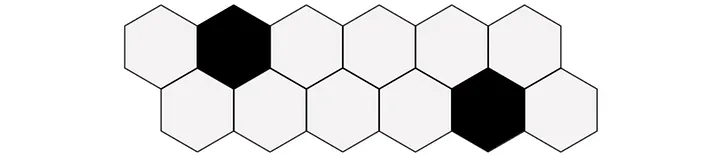
Your tiles cannot occupy the blackened cells in any way. So, to tile the above example, it would have to be done as illustrated below:
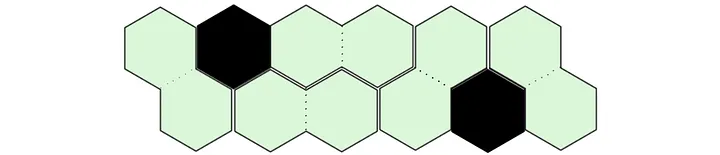
The input is provided to you in the form of two strings, a and b, for each row in the grid. In each string a 0 represents an empty cell, while a 1 represents a blackened cell. The above example is represented like this:
010000
000010
The first line corresponds to string a, while the second line corresponds to string b. You are then required to write a function called hexagonalGrid which takes the two strings as input and returns whether it is tileable or not.
Breaking Down the Problem
In order to simplify the logic, we can first represent the grid as a graph, with grid cells that are adjacent to each other represented by nodes connected together with edges. This would be a more intuitive representation with which we can perform the test, instead of dealing directly with the strings. So we’ll have to parse the string into the graph first.
When trying to parse the graph, an important thing to keep in mind is that the hexagon grid has been transformed into a sort of square grid in the strings a and b, so not all the adjacent cells in the square grid correspond to adjacent cells in the hexagon grid itself.

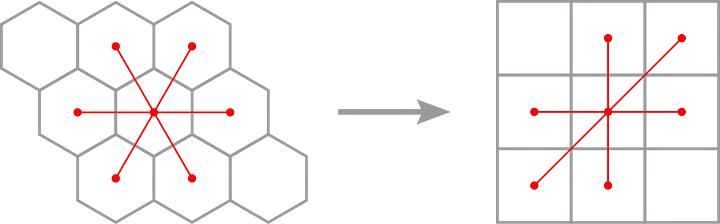
As you can see in the above image, the center cell has six neighbors in the hexagon grid. However, when we shift the cells over into the square grid, the center cell has eight neighboring cells, but only the six highlighted with the connective red lines correspond to cells which it was already adjacent to in the hexagon grid. So, when parsing the graph from the string, we should ignore the adjacent cells in the top-left-to-bottom-right diagonal direction.
Solution
For my solution, I’ll be using TypeScript, but the same concepts should be applicable to whichever programming language you intend to use.
First of all, we define our types for the graph nodes:
/**
* The index of a grid cell in the original strings
*/
type NodeIndex = [number, number];
class GraphNode {
constructor(
public index: NodeIndex,
public connections: Array<NodeIndex>
) {}
/**
* Determines whether the current node is equal to
* some other node based on their `index` values
*/
equals(otherNode: GraphNode): boolean {
return this.indexEquals(otherNode.index)
}
/**
* Determines whether the current node's index is
* equal to some other index
*/
indexEquals(otherIndex: NodeIndex): boolean {
return this.index[0] === otherIndex[0]
&& this.index[1] === otherIndex[1]
}
}
In this snippet, NodeIndex represents the index of the grid cell in the original pair of strings. You can think of it like a (y, x) pair on a coordinate plane. But in this case,“y” is 0 if the cell was in string a, and 1 if the cell was in string b (i.e., y increases downwards). “x” represents the index of the cell in the original string where it is from. As such, a NodeIndex value can be used to uniquely identify each node like an id, but it can also be used to identify the position of the node in relation to the other nodes.
The GraphNode type then includes this as the index of where the node comes from, as well as including the NodeIndex values of all its adjacent connections in the graph.
Here is the function for parsing the graph of nodes from the string:
/**
* Parses the graph of nodes from the hexagonal grid provided in
* the strings a and b
*
* @param a The first line of hexagonal cells
* @param b The second line of hexagonal cells
* @returns A graph of parsed nodes with appropriate connections
*/
function parseNodes(a: string, b: string): Array<GraphNode> {
let results: Array<GraphNode> = []
// Parsing nodes from string a
for (let i = 0; i < a.length; i++) {
if (a[i] === "0") {
results.push(new GraphNode([0, i], []))
}
}
// Parsing nodes from string b
for (let i = 0; i < b.length; i++) {
if (b[i] === "0") {
results.push(new GraphNode([1, i], []))
}
}
// Determining adjacent nodes of each node
return results.map<GraphNode>((value, index, array) => {
let connections: Array<NodeIndex> = []
// Indexes of adjacent cells in all the possible directions in
// which a node can be connected, namely left-right, top-bottom,
// and the top-right-to-bottom-left diagonal direction
let adjacentIndexes: Array<NodeIndex> = [
[value.index[0] - 1, value.index[1]],
[value.index[0] + 1, value.index[1]],
[value.index[0], value.index[1] - 1],
[value.index[0], value.index[1] + 1],
[value.index[0] + 1, value.index[1] - 1],
[value.index[0] - 1, value.index[1] + 1],
]
for (let adjancentIndex of adjacentIndexes) {
let match = array.find(
(element) => element.indexEquals(adjancentIndex)
)
if (match) {
connections.push(match.index)
}
}
return new GraphNode(value.index, connections)
})
}
After extracting the graph of nodes using the above parseNodes function, we then need to determine whether full tiling is possible on that graph. We achieve this using an algorithm whereby, step-by-step, we remove a pair of adjacent nodes from the graph until all the nodes are paired up with one another. If we reach a point whereby it is no longer possible to pair any more adjacent nodes while there are more nodes still remaining, we backtrack and try another combination, as shown below:
When we manage to pair up all the cells, it means that the input grid is tileable, hence answering the original question. Otherwise, it means it is not.
Like most backtracking algorithms, this will be implemented using recursion. The base case of the recursion will be when there are no more nodes left in the graph, but we will also return false immediately if the number of nodes left in the graph is odd.
/**
* Exhaustively attempts to check whether the nodes
* can be paired into the required tiles
*/
function fullTilingIsPossible(nodes: Array<GraphNode>): boolean {
// The recursive base case, when all the nodes have been paired/tiled with another node
if (nodes.length === 0) {
return true
}
// When the number of nodes is odd, it is impossible to tile them in pairs
if (nodes.length % 2 !== 0) {
return false
}
// When you hit a dead end with no new pairings possible
if (!possibleConnectionsExist(nodes)) {
return false
}
for (let node of nodes) {
for (let connection of node.connections) {
if (nodes.some(value => value.indexEquals(connection))) {
// A new list with the two pairable nodes filtered out
let filteredNodes = nodes
.filter((element) => !element.equals(node))
.filter((element) => !element.indexEquals(connection))
// Check whether the remaining nodes can be successfuly tiled
let matchFound = fullTilingIsPossible(filteredNodes)
if (matchFound) {
return true
}
}
}
}
return false
}
The possibleConnectionsExist function referenced above, which tests whether there are any more possible pairings, is shown below:
/**
* Tests whether there are possible connections in a list of nodes
*/
function possibleConnectionsExist(nodes: Array<GraphNode>): boolean {
for (let node of nodes) {
for (let connection of node.connections) {
if (nodes.some((value) => value.indexEquals(connection))) {
return true
}
}
}
return false
}
Lastly, here is the resulting hexagonalGrid function, which should give a higher-level overview of the full algorithm used to solve the problem:
function hexagonalGrid(a: string, b: string): "YES" | "NO" {
// Write your code here
let parsedGraphNodes = parseNodes(a, b);
parsedGraphNodes.sort((a, b) => a.connections.length - b.connections.length);
return fullTilingIsPossible(parsedGraphNodes) ? "YES" : "NO";
}
We parse the graph of nodes from the string, and then we sort them in ascending order of their number of connections so that the testing function should start with nodes that have the least connections. For example, when a node has only one connecting node, it should be obvious that that node should be connected to that particular adjacent node.